Mann Whitney U

Mann Whitney U = A test for difference between two sets of data
---> If we were studying Poole for a long period of time you could conduct a traffic survey at two different times, then use the two sets of results to do a Mann Whitney U test to see if there is a significant difference in the data. This statistical test could then be followed by calculating percentage difference to see how significant the difference is - could be utilised to prove/disprove whether traffic, and therefore congestion, is seasonal in Poole or even before and after the Twin Sails bridge has been built to see if traffic flows across the existing Lifting Bridge have changed.
---> Statistical result of Mann Whitney U is often used to aid the geographical explanation of the distributions mapped
---> Note that whilst result tells us that there is a significant difference, it cannot be used to explain why that difference exists

There are two ways you can do the Mann Whitney U calculation - a non-mathematical way and a slightly more mathematical way. The first is the way we did it in class......
Again, the first stage is to set a null and positive hypothesis:
Positive Hypothesis:- There will be a difference between the two sets of data
Null Hypothesis:- There will not be a difference between the two sets of data
A table is, yet again, the best way to set this statistical test out:
For every piece of data in set X give it a score if it is bigger than a piece of data in B or 0.5 if it is the same:
 - 21 gets a score of 1 as only 23 is bigger than it
 - 12 gets a score of 7.5 as 23, 18, 17, 17, 13, 20 and 14 are bigger than it, giving it 7 and it is equal to 12, adding an extra 0.5. Thereby bringing its total to 7.5
Then you simply do the same, but in reverse , for data set Y: Add up the totals and take the smaller of the two totals as your U value:

Mann Whitney U is unusual as it is the only stats test where your result has to be smaller than the critical value to be significant. You can also have two data sets with differing amounts of data within.
Critical Value for 10 values in each data set is 23 so this difference is not statistically significant so we have to accept the null hypothesis.
The second, more mathematical way honestly looks a lot worse than it actually is, although if you are comfortable with using the above method, it is probably best to stick to that one (I probably will!), so this is just for those of you who are interested - I am going to use the first example we did in class......

First, rank all the values for both samples from the smallest (=1) to the largest, ranking samples the same way you do in Spearman's Rank if more than one is the same:

Total the ranks in each column:

Calculate the U values for both samples using the following formula [Note that na in formula should be larger sample size if difference is present]:
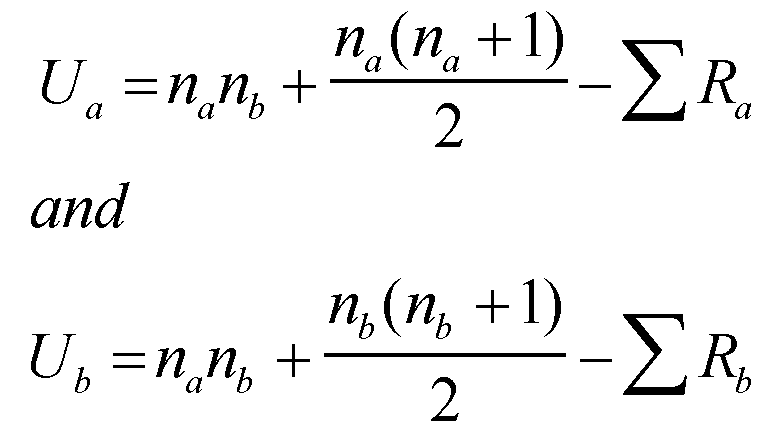Ua = (10x10) + (10x11) - 70
                               2
= 85

Ub = (10x10) + (10x11) - 137
                                2 
= 18
Then you compare the lowest result to the critical values; this is below 23 and so the positive hypothesis can be accepted.

Well, I am nearly there with all the stats test - the last, Chi Squared, will probably appear sometime tomorrow!!!